Do you know about Answer Set Programming?
How much code do you need for a sudoku solver in a programming language of your choice? Using answer set programming (ASP), seven lines of fairly readable code suffice.
A common approach to solving a problem using the ASP paradigm is generating a set of candidate solutions and restricting that set to valid solutions. The framework will to the searching for you. So you do not describe how to search for the solution, but only what a solution looks like (there may be 0, 1 or many; using solver parameters indicate if you are happy with one or if you want to see all…). (Every fact in the solution must have a valid derivation using the given program.)
You can find the original code here. I made some small changes.
Here is the program.
number(1..9).
square(R, C) :- number(R), number(C).
1 { numberAt(R, C, P) : number(P) } 1 :- square(R, C).
:- numberAt(R, C1, P), numberAt(R, C2, P), C1 != C2.
:- numberAt(R1, C, P), numberAt(R2, C, P), R1 != R2.
cubeColor(F,RC,P) :- F := (((C-1)/3)+(3*((R-1)/3))),RC:=(10*R+C),numberAt(R, C, P).
:-cubeColor(F,RC1,P),cubeColor(F,RC2,P), RC1!=RC2.
What do these rules mean?
number(1..9).:
number is the predicate that tells us whether something is a number or not. 1, 2,…, 9 are numbers. They are our domain constants for defining positions and the entries themselves. This is actually a short version for number(1), number(2), ...
square(R, C) :- number(R), number(C).:
square is the predicate that tells us whether the pair of two things is a position or not. Head:-Body. is what a rule generally looks like and it states that if the Body is evaluated to true, then the Head is evaluated to true. If R(ow) and C(olumn) are numbers, then (R,C) is a square, i.e. a valid position for an entry.
1 { numberAt(R, C, P) : number(P) } 1 :- square(R, C).:
This rule needs a bit more explanation. numberAt(R,C,P) is the predicate that tells us whether P is the number in row R and column C. The translation of the above rule is: at each square there is exactly one number. So how does the rule work? Using the prior rules, we can derive that e.g. square(3,4) is true, so 1{numberAt(3,4,P):number(P)}1 must be true as well. 1{...}1 is a cardinality constraint requiring exactly one of the predicates within the braces to hold (i.e. one must be true, all the others must be false). numberAt(3,4,P):number(P) is a short hand notation for numberAt(3,4,1), numberAt(3,4,2),... numberAt(3,4,9), because those are the constants for which the number predicate holds.
So these three rules create our candidate solutions: a 9x9 matrix, with exactly one number at each position. Now we have to narrow that down to valid make it a valid solution.
:- numberAt(R, C1, P), numberAt(R, C2, P), C1 != C2.: Here the rule head is missing, which means, if the body evaluates to true, the search fails. So, if the same number appears in the same row in different columns, then we do not have a solution. An analogous rule exists for numbers in the same column.
The last two rules deal with numbers within the 3x3 sub fields of a sudoku.
cubeColor(F,RC,P):- F := (((C - 1) / 3) + (3 * ((R - 1) / 3))), RC:=(10 * R + C), numberAt(R, C, P).: RC is a simple single number encoding of a position (10 times the row number plus column number). F is an encoding for the 3x3 field calculated from row and column. So cubeColor is a predicate describing the numbering within the 3x3 field.
:-cubeColor(F,RC1,P), cubeColor(F,RC2,P), RC1!=RC2: Whenever the same number appears in the same 3x3 subfield at different positions the search fails.
If you want a particular sudoku solved, you simply add facts describing your sudoku instance in the form numberAt(1,3,7) etc.
There is an eclipse IDE for ASP - SeaLion. You can download a standalone version or install it via an update site (solvers included). The system includes the possibility for visualising solutions - via an ASP program. I did not find too much documentation for that feature, so the following program for doing that may not be too elegant.
%place numbers
vistext(10*X+Y,Z):-numberAt(X,Y,Z).
visposition(10*X+Y,20*X,20*Y,10):-numberAt(X,Y,Z).
viscolor(10*X+Y,black):-numberAt(X,Y,Z).
%Grid
visgrid(sud,9,9,400,400).
visposition(sud,8,12,-1).
%single rectangle
visrect(empty,20,20).
visbackgroundcolor(empty,white).
viscolor(empty,lightgray).
%fill grid with gray rectangles
g(1..9).
visfillgrid(sud,empty,X,Y):-g(X),g(Y).
%3x3 fields bold
f(-1;0;59;60;119;120;179;180).
%horizontal lines
visline(200+X,13,17+X,192,17+X,1):-f(X).
viscolor(200+X,black):-f(X).
%vertical lines
visline(400+X,13+X,16,13+X,197,2):-f(X).
viscolor(400+X,black):-f(X).
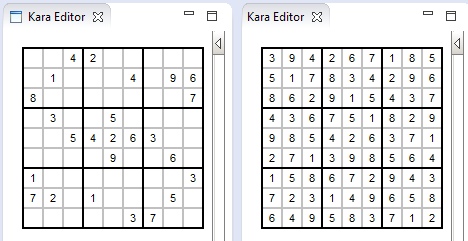
Given the evil sudoku instance from Joel, the result of solving and visualising looks as follows: